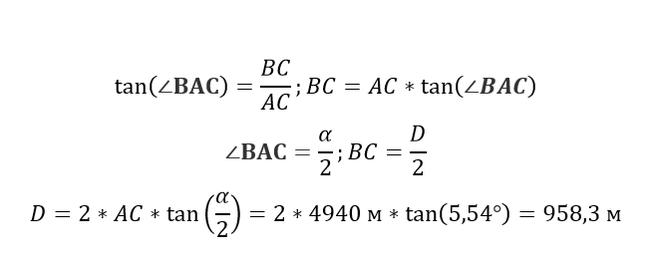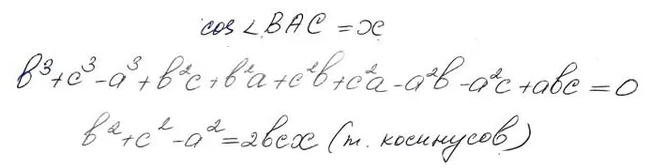Решение этой задачи блин

Задача «Блины»

Мы все знаем, что начавшаяся зима скоро закончится, и на праздновании Масленицы все будут есть блины. Об этом и будет наша задача.

N гостей сидят за столом, и перед каждым стоит тарелка с блинами. На тарелке i-го гостя лежит ai блинов. Каждый гость съедает один блин за одну минуту, таким образом, время, когда закончит есть блины последний человек, равно наибольшему значению из ai.

Неожиданно к ним присоединился ещё один человек, и теперь все присутствующие могут переложить часть своих блинов (в том числе могут переложить все свои блины, а могут не перекладывать ни одного блина) вновь пришедшему человеку. Перекладывание блинов происходит одновременно и моментально.

Гости хотят переложить блины таким образом, чтобы после перекладывания они съели все блины за минимальное время (которое равно наибольшему числу блинов на тарелках у гостей, включая нового гостя). Определите, за какое наименьшее время гости смогут съесть свои блины после перекладывания.

Программа получает на вход натуральное число N, не превосходящее 100.000, – первоначальное количество гостей. Следующие N строк содержат натуральные числа ai – количество блинов на тарелке i-го человека. Значения ai даны в порядке неубывания, то есть ai ai+1. Сумма значений всех ai не превосходит 2109.

Программа должна вывести одно целое число – минимальное время, за которое все гости закончат есть свои блины после перекладывания части блинов на тарелку нового гостя.

Ошибка в коде (задача «частотный анализ»)
Имеется следующая задача: Дан текст. Выведите все слова, встречающиеся в тексте, по одному на.

Задача «Вывести маршрут максимальной стоимости»
Здравствуйте, помогите пожалуйста с решением задачи 🙂 В левом верхнем углу прямоугольной.

Задача «Часы с боем» , Python
Здравствуйте! Вчера на отборочном туре я неудачно пыталась решить задачу «Часы с боем». На её.

Задача «Больше своих соседей»
Дан список чисел. Определите, сколько в этом списке элементов, которые больше двух своих соседей и.

Задача «Самое частое число»
Дан список. Не изменяя его и не используя дополнительные списки, определите, какое число в этом.

Задача из книги «A Byte of Python»
Здравствуйте. Возник ряд вопросов по заданию из книги. Вот задание: Наиболее важным.

задача: «Шварценеггер против Годзиллы»
Нужно укоротить код, для уменьшение времени выполнения программы, дается 1 секунда, а выполняется.

Задача: «Квадратов много не бывает»
Помогите пожалуйста, ни как не могу понять, что не получается. Задача взята с сайта. Задача.

Источник

Задачи по математической грамотности

Ищем педагогов в команду «Инфоурок»

Практическая работа № 3

«Разработка заданий по математической грамотности»

5 класс. Действительные числа (задача из книги Я. Перельмана)

Мой заработок за последний месяц вместе со сверхурочными составляет 250 рублей. Основная плата на 200 рублей больше, чем сверхурочные. Как велика моя заработная плата без сверхурочных?

1. Область содержания – неопределенность и данные

2. Компетентностная область оценки – рассуждать и формулировать

3. Контекст – личный

4. Уровень сложности – легкий

5. Формат ответа – развернутый ответ

6. Объект оценки – нахождение заработной платы

7. Система оценивания — 1 балл(неполный ответ),2 балла(полный ответ), 0 баллов (ответа и решения нет).

Если к сверхурочным прибавить 200 руб., то получим основную заработную плату. Поэтому если к 250 руб. прибавить 200 руб., то у нас должны составиться две основные зарплаты. Но 250 + 200 = 450.

Значит, двойная основная зарплата составляет 450 руб. Отсюда одна зарплата без сверхурочных равна 225 руб., сверхурочные же составят остальные от 250 руб., т.е. 25 руб.

Проверим: заработная плата, 225 руб., больше сверхурочных, т.е. 25 руб., на 200 руб., как и требует условие задачи.

6 класс. Действия с десятичными дробями. Умножение и деление десятичных дробей. Обычная лампа накаливания потребляет электроэнергию 60 Вт ⋅ ч, а энергосберегающая лампа – 12 Вт ⋅ ч. Сколько рублей в месяц составит экономия от снижения потребления электроэнергии при замене простой лампы накаливания на энергосберегающую лампу? Если лампа будет работать 6 часов в сутки. Стоимость электроэнергии в квартире с электрической плитой при однотарифном счетчике составляет 4 руб. 10 коп. за 1 кВт ⋅ ч. Принимаем, что в месяце 30 дней. За какой срок окупится энергосберегающая лампа, если ее стоимость составляет 98 руб. 2 коп., а стоимость лампы накаливания – 27 рублей.

1. Область содержания – неопределенность и данные

2. Компетентностная область оценки – рассуждать и формулировать

3. Контекст – личный

4. Уровень сложности – сложный

5. Формат ответа – развернутый ответ

6. Объект оценки – расчет коммунальных платежей

7. Система оценивания — 1 балл (неполный ответ),2 балла(полный ответ), 0 баллов (ответа и решения нет).

1) 60 × 6 = 360 Вт ⋅ ч – за 6 ч/сутки потребляет обычная лампа;

2) 12 × 6 = 72 Вт ⋅ ч – за 6 ч/сутки потребляет энергосберегающая лампа;

3) 360 × 30 = 10800 Вт ⋅ ч = 10,8 кВт ⋅ ч – в месяц потребляет обычная лампа; Раздел 1. Личный финансовый план 22

4) 72 × 30 = 2160 Вт ⋅ ч = 2,16 кВт ⋅ ч – потребляет в месяц энергосберегающая лампа;

5) 4,10 × 10,8 = 44,28 рублей – нужно заплатить за месяц при использовании обычной лампы;

6) 4,10 × 2,16 = 8,86 рублей – нужно заплатить за месяц при использовании энергосберегающей лампы;

7) 44,28 – 8,86 = 35,42 рублей составит экономия от использования 1 энергосберегающей лампы в месяц.

8) Если вместо перегоревшей лампы накаливания мы поставим энергосберегающую лампу, то: (98,02 – 27,0) : 35,42 = 71,02 : 35,42 = 2,00508 т.е. энергосберегающая лампа окупится за 3 месяца.

Ответ: 35,42 рублей, за 3 месяца.

Мама решила связать шарфы для сына и дочки. Для этого она купила 800 г разноцветной шерстяной пряжи. Размеры шарфа для сына: 30 см ширина, а длина 1,8 м. Для шарфа дочери необходимо ввязать два прямоугольника, длиной 1 м и шириной 50 см. На шарф сына у мамы ушло 300 г пряжи. Хватит ли ей пряжи, чтобы связать шарф для дочери?

1. Область содержания – количество, пространство и форма

2. Компетентностная область оценки – формулировать и применять

3. Контекст – личный

4. Уровень сложности – средний

5. Формат ответа – развернутый ответ

6. Объект оценки – определение количества оставшейся пряжи

7. Система оценивания — 1 балл (неполный ответ),2 балла(полный ответ), 0 баллов (ответа и решения нет).

1)0,5*1*2 = 1 (м 2 ) – площадь шарфа для дочки

2) 0,3*1,8=0,54 (м 2 ) – площадь шарфа для брата

3) 300:0,54≈556(г) – нужно для вязания шарфа дочки

4) 800-300 =500 (г) – осталось пряжи

Ответ: не хватит

7 класс. График функций (ВПР 7 класс, ОГЭ 9 класс).

Уровень годовой инфляции в России в 2007-2018 годах показан на диаграмме.

Определите по графику:

1. Периоды низкой инфляции.

2. Периоды высокой инфляции.

3. Во сколько раз инфляция 2008 года была выше инфляции 2017 года?

4. Во сколько раз инфляция 2015 года была выше инфляции 2017 года?

1. Область содержания – изменения и зависимости

2. Компетентностная область оценки – рассуждать и применять

3. Контекст – общественная деятельность

4. Уровень сложности – средний

5. Формат ответа – краткий ответ

6. Объект оценки – исследование графика инфляции России

7. Система оценивания — 1 балл за каждый верный ответ, 0 баллов за неправильный ответ.

1) 2017–2018 года.

2) 2007–2008, 2014–2015 года.

3) 13,28 / 2,52 = 5,27 раз.

4) 12,91 / 2,52 = 5,12 раз.

Ответ: 1. 2017–2018 года. 2. 2007–2008, 2014–2015 года. 3. 5,27 раз. 4. 5,12 раз.

(6 класс логические задачи)

Старинные часы, которые висят при входе в музей, отстают на 30 с в сутки. Директор попросил часовщика отрегулировать часы так, чтобы они отставали на более чем на 5 мин, если их не регулировать каждый день. Как часовщику придется регулировать эти часы? Отметьте один верный вариант ответа и объясните его.

· Каждые 2 недели

1. Область содержания – неопределенность и данные

2. Компетентностная область оценки – рассуждать и применять

3. Контекст – общественная деятельность

4. Уровень сложности – средний

5. Формат ответа – выбор нескольких верных ответов

6. Объект оценки – регулирование часов

7. Система оценивания — 1 балл за верный ответ и рассуждение, 0 баллов за неправильный ответ.

1) За сутки часы отстают на 30 секунд; 5 минут=5*60=300 сек, 300:30=10 суток

2) Если часы отстают на в сутки на 30 секунд, то за 2 суток -1 минута, 10 суток – 5 минут.

3) 5 минут= 30сек, 300:30=10 суток

4) Отстают на минуту за 2 суток, на 5 минут – 5*2=10 суток.

(5 класс, логические задачи)

В блинной продаются блины одной и той же толщины, но двух разных размеров. Блин диаметром 20см стоит 20 рублей, а блин диаметром 40 см – 40 рублей. В блин можно завернуть любую начинку на выбор: варенье, мясо, творог, сгущённое молоко. Блин можно взять с собой в случае, если он упакован в конверт.

Выберите верное утверждение.

· Если 10 г варенья уходит на то, чтобы полностью покрыть одну сторону блина диаметром 20 см, то на блин диаметром 40 см уйдет 40 г варенья.

· Если одной банки варенья хватает на то, чтобы полностью покрыть одну сторону 40 блинов, то этой банки хватит на 10 блинов диаметром 20см.

1. Область содержания – количество, пространство и форма

2. Компетентностная область оценки – рассуждать

3. Контекст – общественная деятельность

4. Уровень сложности – средний

5. Формат ответа – выбор нескольких верных ответов

6. Объект оценки – определение количества варенья

7. Система оценивания — 1 балл за верный ответ, 0 баллов за неправильный ответ.

9 класс (подготовка к ОГЭ)

В таблице приведены размеры штрафов, установленные на территории России с 1 сентября 2013 года, за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации.

Источник

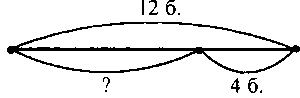
ГДЗ по математике, 2 класс, Моро М.И. Сколько блинов съели за обедом?

Бабушка испекла 12 блинов. После обеда осталось только 4 блина. Сколько блинов съели за обедом?

12-4 = 8 (б.) Ответ: 8 блинов.

1) Запиши 3 любых двузначных числа. Умень-
ши каждое из них на 10.
2) Запиши 3 любых однозначных числа. Уве- ( Подробнее. )

Оля перепрыгнула через верёвочку 18 раз, а
Света — только 10 раз.
Поставь вопрос и реши задачу.

Кто сможет? Выполните деление:
( Подробнее. )

Троллейбус за время t прошел путь s. Какую скорость v приобрел он в конце пути и с каким ускорением а двигался, если начальная скорость ( Подробнее. )

Put the verbs in brackets in the present simple or the present continuous. Give reasons.
1 A: Why . ( Подробнее. )

Источник

Как объяснить четвероклашке решение этой задачи?

Эта задача от моих зрителей. Её предлагают решить ученикам в 4 классе. Разносторонний треугольник с периметром 180 разделён отрезками так, что внутри образовалось 9 треугольников, при чём, с равными периметрами. Чему равен периметр каждого маленького треугольника. Задача просто решается с помощью формулы и составления уравнений, но в 4 классе не учат делать ни то , ни другое. Как решить такую задачу и объяснить её ученику 4 класса?

Здравствуйте ! Попыталась решить «наскоком»:

На сторонах большого треугольника лежит 9 сторон маленьких треугольников. В общей сумме 180. Значит «средняя арифметическая» сторона равна 20. Соответственно, периметр любого малого треугольника равен 20*3=60.

Но вот чувтвую, что решение это скользкое, поэтому пытаюсь решить по-другому:

Обозначаю все стороны малых треугольников, лежащих на сторонах большого, как

а все стороны малых треугольников, лежащих внутри большого, как

и суммирую через эти обозначения периметры малых треугольников. При перестановке этих обозначений в выражении в более красивый вид получаем:

Для «наружних» малых треугольников (те, чьи стороны лежат на сторонах большого треугольника), а их 6, получаем:

А для «внутренних», чьи стороны не лежат на сторонах большого, а их 3, получаем:

Делаем вывод, что б1+б2+. б9= а1+а2+. +а9=180, а это три равных по периметру «внутренних» треугольника.

Получаем периметр малого — 60.
Не уверена, что таким образом можно объяснять четвероклассникам. До Вашего метода не дошла — поленилась, уже поздняя ночь !

Вот какая мысль пришла при решении этой задачи:

Если указать координаты вершин большого треугольника, то каковы будут координаты серединной точки ? Всех вершин треугольников ? Уверена, эта задача легко будет решена с помощью простой программы для компьютера.

Спасибо Вам, было занимательно напрячь свои мозги. Но если честно, я своим результатом не очень довольна. Грусть.

Сумма всех получившихся отрезков (и внутренних и внешних) равна периметру шести маленьких треугольников. Это видно если временно вычеркнуть три центральных треугольника, у которых стороны не лежат на сторонах внешнего треугольника.

В тоже время если складывать отрезки всех девяти треугольников, то все внутренние отрезки будут учтены дважды. Но мы можем и внешние учесть дважды ,просто добавив к сумме их общую длину — периметр большого треугольника равный 180.

Вот и получается что два раза по шесть (12) треугольников — это тоже самое что и девять треугольников да ещё 180. Т. е. На 180 приходится 12-9 = три треугольника. Тогда периметр одного треугольника — 180:3 = 60

Спасибо. Отчего-то пришёл в голову вариант, что большой треугольник можно сложить шесть раз для получения девяти маленьких треугольников.

Решение инженерной задачи с помощью тригонометрии

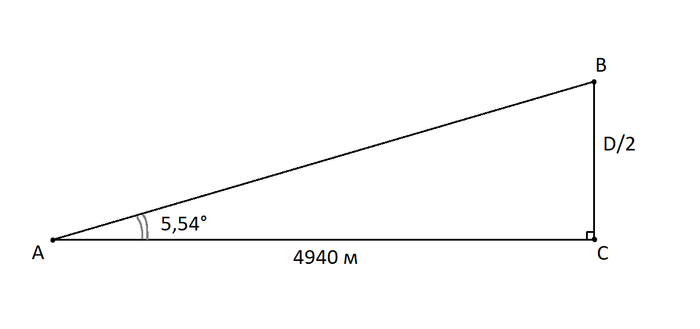
Спасение хвостового оперения самолётов

Реактивная струя из моторов первых реактивных

самолётов сжигала хвостовое оперение. Но конструкторы предложили слегка повернуть моторы (на небольшой угол a).

Найти величину гипотенузы, пользуясь только знаниями семиклассника

Задача не сложная для старшеклассника, но у семиклассника пока нет полного набора инструментов, который делают это задачу лёгкой, поэтому надо учиться думать.

Как древние греки вычислили длину окружности Земли

Коротко и наглядно о том, как древнегреческий математик и астроном Эратосфен Киренский вычислил размеры Земли ещё в III веке до нашей эры.

Удвоить угол с помощью двусторонней линейки

Построение с помощью двусторонней линейки относится к типу задач на построение ограниченными средствами. При этом, линейка наделяется несколькими волшебными свойствами. Её противоположные стороны параллельны и идеально ровные, 3 и 4 стороны линейки нельзя использовать (тем более для построения прямых углов) и даже если на линейке есть мерные деления, мы не используем их для решения задач.

Построить с помощью двухсторонней линейки прямой угол

Это геометрическая задача, которую можно назвать головоломкой. Необходимо построить прямой угол используя только двухстороннюю линейку, при этом обвести уголок линейки-не вариант и мерными делениями линейки то же не надо пользоваться))).

Школьники не смогли решить заданную Мишустиным задачу

1 сентября 2021, 13:04Текст: Алексей Дегтярев
Премьер-министр Михаил Мишустин в ходе визита в физтех-лицей имени Капицы на День знаний на уроке одиннадцатиклассников задал им физтеховскую задачу.
Глава правительства вошел в класс с букетом цветов, он вручил их преподавателю математики Ольге Браславской, ученики в этот момент решали задачу по анализу бизнес-проектов, передает РИА «Новости».
«Зачем же в физтехе бизнес-проектами заниматься, ребята? Здесь нужны фундаментальные знания, правильно?», – обратился к учащимся премьер.
«В современное время нужны специалисты на все руки, особенно в России», – ответили ученики.
Мишустин на доске начертил задачу для школьников, он предложил провести перпендикуляр от точки окружности к диаметру, не используя никаких измерительных приборов, и дал время на ее решение, сообщив, что зайдет позднее.
Школьники начали бурно обсуждать задачку и искать ответ, но не смогли справиться с ней.
Мишустин вернулся в класс и раскрыл решение задачи, подкрепив его ответом на доске.
«Конечно, очень важно решать задачи, связанные с бизнесом, и с приложением математических фундаментальных знаний, которыми вы обладаете. Но мне кажется, в вашем возрасте хорошо бы фундаменталки поднабраться. А когда вы будете обладать математическими знаниями, физикой, химией, вы сможете решать любые задачи, включая бизнес», – сказал премьер.
Напомним, Мишустин в День знаний посетил физтех-лицей имени Капицы, который находится в подмосковном Долгопрудном. Обучение в вузе ведется с 5 по 12 классы. С 2015 по 2021 годы лицей выпустил 94 медалиста, 85 победителей и призеров заключительного этапа Всероссийской олимпиады школьников, 45 победителей и призеров международных олимпиад.

Каких размеров Селестия и как далеко она находится | Genshin Impact

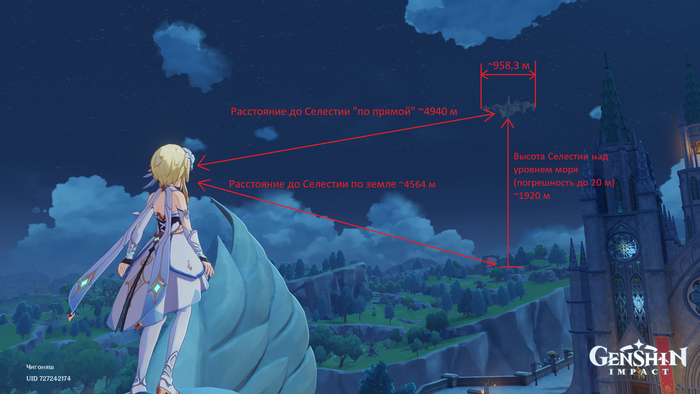
Пожалуй каждый, кто играл в Genshin Impact замечал парящий архипелаг на западе от Монштадта. Эти острова — Селестия, место где живут (или могут жить) архонты, боги истоков и обычные боги. И несмотря на то, что она находится за пределами карты, а также расположена выше любого объекта в Тейвате, её размеры, высоту над уровнем моря и расстояние до неё можно измерить, а точнее вычислить. Об этом и будет этот пост. Ну а для тех, кто хочет сразу же получить ответ — держите картинку со всем, что будет вычислено далее

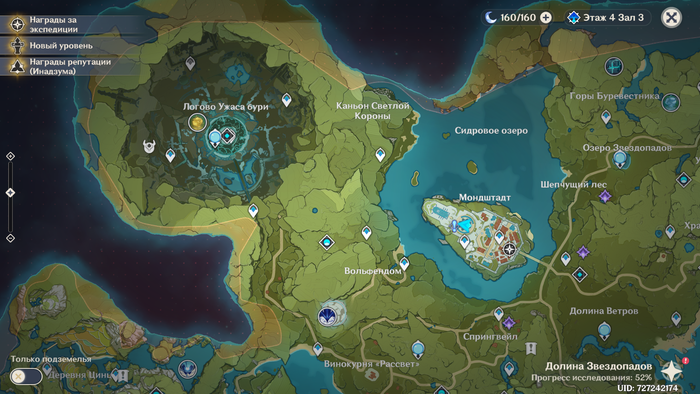
Ну а теперь приступим к самим вычислениям. Для измерений будет использоваться 2 точки: одна в Монштадте, на голове статуи анемо-архонта, другая возле логова Ужаса Бури. Точки эти находятся приблизительно на одной с Селестией прямой, поэтому погрешность при измерении будет несущественная. Вот эти самые точки: маркер игрока — точка в Монштадте, метка возле логова Двалина — 2 точка

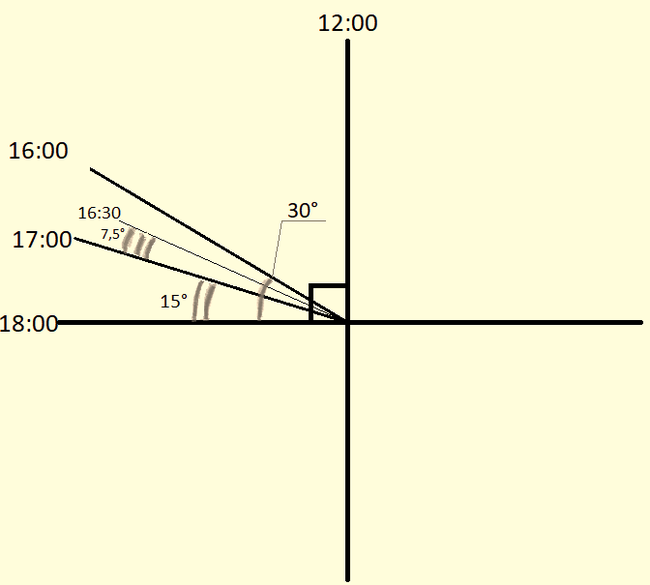
Для начала стоит определить, какие данные у нас есть. Во-первых, мы знаем расстояние между этими точками. Определить его легко: сначала при помощи метки задания определяем масштаб карты, а затем измеряем расстояние между точками замера. Я это делал линейкой (если точнее — рейсшиной) и калькулятором. Также мы можем измерить угол над горизонтом для Селестии (для простоты понимания такая аналогия: у нас есть 2 луча, начала которых образуют угол, мы можем крутить этот угол (т.е. менять его значения), и вот когда один луч будет смотреть ровно в горизонт, а второй — в Селестию, то это и будет угол над горизонтом). Измерить его можно по Солнцу. Так как угол падения солнечных лучей изменяется +- линейно, то, зная время, когда Солнце находится ровно за Селестией, можно определить, какой угол у Селестии над горизонтом. По картинке ниже вы можете понять, как я это делал (в Монштадте Солнце было позади Селестии в

16:30, возле логова —

Еще можно измерить угловой размер Селестии, но об это позже
И так, у нас есть необходимые данные: расстояние между точками замера 1289,6 м, угол над горизонтом в Монштадте

22,5°, возле логова Ужаса Бури

30°.
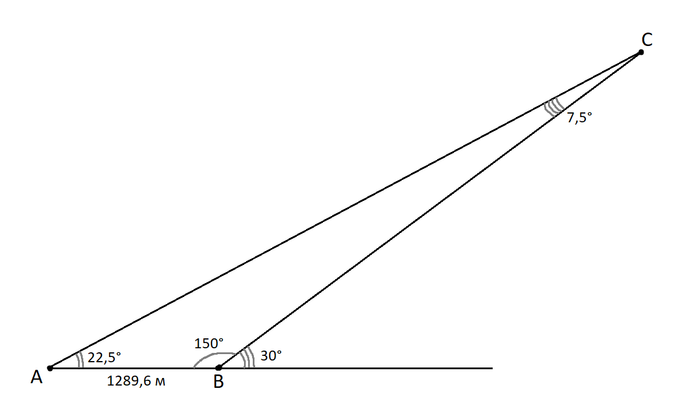
Теперь можно начинать рассчитывать расстояние до этогих парящих островов. И в этом нам поможет тригонометрия. Итак построим треугольник ABC, где A — первая точка замера, B — вторая точка замера, C — Селестия

Пожалуй, объяснять, как были определены углы ACB и ABC нет смысла, это и так понятно. А теперь вспомним немного тригонометрии, а точнее — теорему синусов. Дальнейшие вычисления — картинка из ворда, к сожалению Пикабу не дает написать обыкновенную дробь

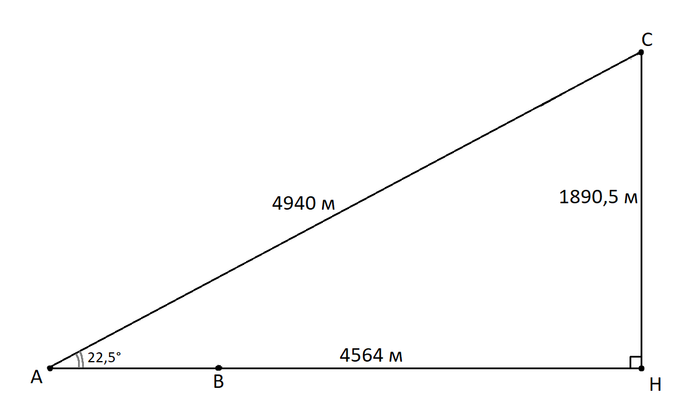
АС — расстояние от Монштадта до Селестии по прямой. Теперь мы можем определить, на какой высоте находится Селестия и сколько нужно идти по земле, чтобы оказаться ровно под нею. Для этого проведем высоту CH к прямой AB. Мы получим прямоугольный треугольник.

Так как нам известен один из углов при гипотенузе и длина гипотенузы, то используя синус и косинус можно найти оба катета. И сейчас вы могли заметить, что длина высоты CH не равна той высоте, которая была указана на картинке в начале поста. Но на самом деле к найденной высоте нужно прибавить высоту над уровнем воды для точки замера (значение этой высоты я определял на глаз, поэтому она имеет значительную погрешность, однако при таких относительно больших расстояниях эта погрешность не оказывает значительного на точность результата)
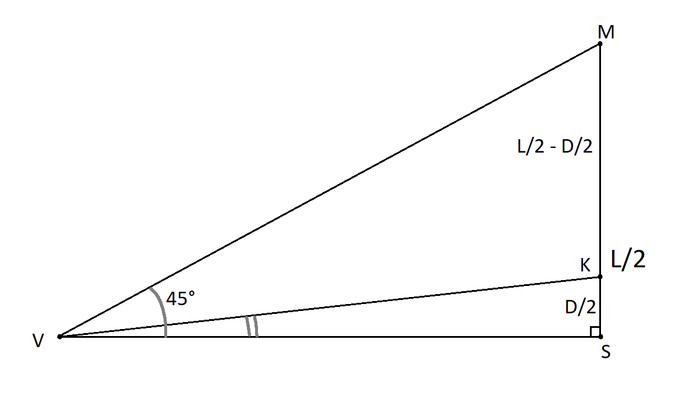
А теперь приступим к измерению размеров Селестии. Для этого нужно узнать ее угловой размер. А как его измерить? В Genshin Impact FOV равен 90°, при этом по краям изображение искажается не сильно, что нам на руку. Измерим длину монитора (длину изображения на мониторе) и длину изображения Селестии. Поскольку искажением изображения по краям можно пренебречь, построим треугольники VMS и VKS и составим уравнения (D — длина изображения Селестии, L — длина монитора)

И так, угловой размер Селестии (при взгляде из Монштадта) равен 2*∠SVK = 11,08°. Ну и теперь приступим к последнему построению за этот пост. Нам нужен прямоугольный треугольник ABC (D — размер Селестии, можно сказать ее диаметр, α — угловой размер Селестии)

Итак, теперь мы знаем как далеко находится Селестия и каких она размеров. И подытожить все проделанные вычисления можно картинкой из начала поста. Стоит отметить, что если она будет добавлена в игру как локация, то скорее всего будет схожа с подземельями: снаружи небольшие, внутри огромные. Но так или иначе Селестия — самый крупный населенный пункт (если так его можно назвать) из доступных, и при этом она не так уж сильно удалена от нас (например Инадзума находится в более чем 6 км от Монштадта)
Ну и на этом все, пишите свои способы вычислить расстояние до нее (если этим вообще кто-то занимается или занимался)

Единственный в своём роде треугольник Шарыгина, открытый лишь в 1982 году

Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать об удивительном геометрическом объекте, впервые рассмотренным советским математиком Игорем Федоровичем Шарыгиным.

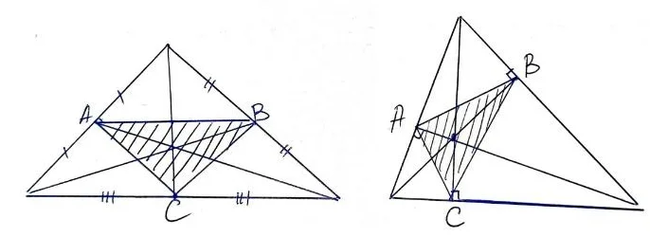
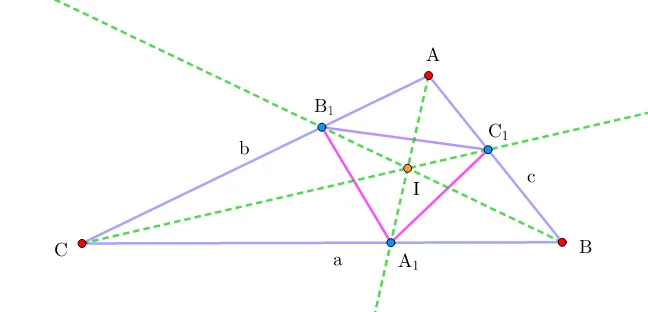
Для начала посмотрите на рисунок ниже. Что Вы на нём видите?

Объясняю: слева заштрихован треугольник, вершины которого образованы основаниями медиан (делят сторону пополам), а справа — основаниями высот. Если большие треугольники не являются равнобедренными, то и заштрихованные равнобедренными быть не могут, это доказанный факт.

Но, погодите, есть же еще биссектрисы!

И тут становится интересно! Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным!

Заметка Шарыгина об этом объекте опубликована в книге «Задачи по геометрии. Планиметрия», 1982.

Впрочем, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!

Основная суть доказательства сводится к рассмотрению подобных треугольников и применению теоремы косинусов, что позволяет получить вот такие выражения для сторон треугольника:

Дальнейшие разборки — дело для настоящих ценителей вкуса. Придется делить уголком, решать квадратные и не очень уравнения, использовать неравенство треугольника, да и вообще немного поднапрячься, чтобы получить результат.

Интересный факт: треугольники Шарыгина могут быть и с целочисленными сторонами. Однако, минимальный из них — (1 481 089, 18 800 081, 19 214 131).

Самим доказательством (доступным каждому школьнику 9 класса!) можно проникнуться в телеграмм-канале «Математика не для всех».

Тригонометрия на пальцах

Ответ на пост «Гифка с фурами нервно курит в сторонке»

Больше фракталов богу комплексных чисел!

Рациональные неравенства. Метод интервалов | Математика

Сегодня мы научимся решать неравенства методом интервалов. определять чётность корней и знаки на промежутках.
Приятного просмотра!

Графическое решение уравнений | Математика

В новом уроке мы научимся находить решения уравнений, просто построив графики.

Первообразная функции. Определение. Таблица | Математика

В новом видео мы дадим определение первообразной, рассмотрим таблицу первообразных для вычисления.

Определение вектора в пространстве. Модуль вектора, равенство векторов | Математика

В этом видео мы дадим определение и координаты вектора в пространстве. Научимся считать его модуль.
Приятного просмотра!

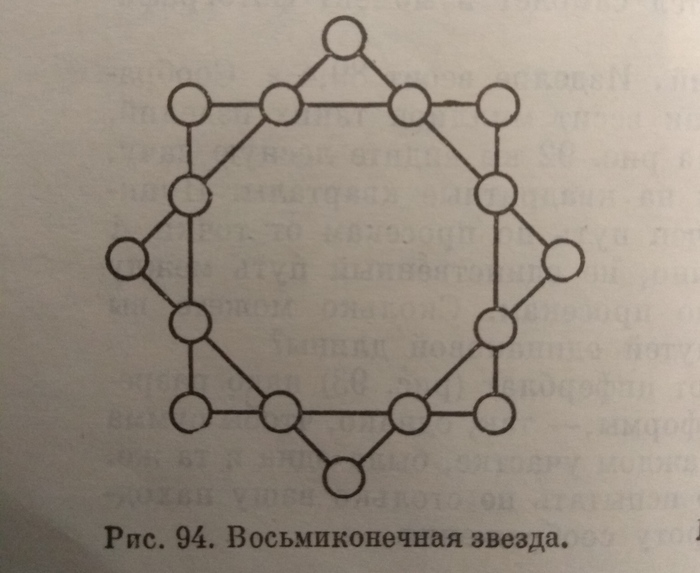
Математическая звезда

Мама с этого года на пенсии (трудилась инженером почти до 66!). Третий месяц смотрит телевизор, играет в игрушки на телефоне, кашеварит, гуляет по магазинам (последние 2 недели, правда, не выпускаем), в общем все, как положено! Недавно застал ее с советской книжечкой «нам не скучно» для детей — порешивает себе понемногу задачки, чтоб разминать извилины — похвалил.

Примерно неделю назад захожу на кухню. Все как обычно: смотрит сериалы про гадалок, решает задачки. Поинтересовался текущей научной составляющей ее досуга. Вот она.

Дело было вечером, делать было нечего..

Сел рядом, взял листок, карандаш, попытался раз, другой, пятый, девяносто девятый.. Не получается. Нашел 16 фишек, пронумеровал, начал тасовать поверх нарисованной схемы. Так был убит первый вечер.

На следующий день мама переняла метод тасования фишек, а я подумал, что от безделья можно попытаться написать программу. И хотя последний раз я программировал в ЖВбейсике почти 25 лет назад, мою решимость подстегнула неизбежность новой встречи с информатикой — сын тоже начинает свой путь в мире информационных технологий в соответствии со школьной программой, а она (школьная программа) зачастую (в особенности в период карантина) ложится на мои уставшие плечи. Глянул часовое видео на Ютубе о Python, скачал приложение на телефон.. Так я убил второй вечер.

В конце недели в гости приехала сестра — скучно сидеть на карантине в одиночестве. До ее приезда созданный мной код-фракенштейн (при написании я в наглую копировал из сети готовые участки) успел перебрать 550 млн комбинаций, после чего был дисквалифицирован за затяжку времени, а я решил заняться более полезными (пикабушку листал 2 дня) делами. А что сестра? Даром, что врач, хоть и временно безработный. Врачам сегодня заняться нечем? Тоже садится расставлять циферки по кружочкам. А где двое, там и третий — мне же опять интересно! Так группой из трёх лиц по предварительному сговору был убит очередной вечер..

Закончилась та неделя, у сына закончились каникулы ( Побочки дистанционного обучения на карантине ),у жены закончился отпуск (почему-то рабочий день на удалёнке теперь 12 часов, завтра в шесть вечера пойду к щитку вырубать автомат, чтоб не наглели), сестра уехала домой, мне тоже надо работу работать в перерывах домашнего обучения сына, мамины фишки от миллионов перемещений стёрлись в пыль. А задача для школьников 5-9 классов осталась. Нерешённой. Тремя взрослыми с высшим образованием.

Решение в книге приводится, но никто из нас смотреть его не стал. Для меня, собственно, вопрос не в том, как случайным образом расставить числа в кружочки (таких расстановок 16! — это более 2 триллионов комбинаций). Меня интересует, можно ли эту задачу решить математически (сузить количество перебираемых вариантов до разумных пределов). А также, сколько уникальных решений имеется всего (думаю, если в решении, приводимом в книге, заменить числа по принципу: 1 на 16, 2 на 15, 3 на 14. — это не стоит считать уникальным решением).

Если есть здесь любители повозиться с головоломками (вообще-то не сомневаюсь, что есть!), делитесь вашими соображениями!

Источник

Мне нравитсяНе нравится